Right so what ways can we use to check:
Single Parity - Odd
In the example of ASCII which we used in an earlier post we can can check for errors using the 8th digit.
This works by changing the 8th digit to make all the 1's = an odd number
so when we look back at all the strings in the object we are checking we can see if all the bytes = odd numbers, if not then we know that a bit has been changed.
in the same way we can use the even system which also uses the same system but you change the 8th digits to make the bytes = even numbers.
Right so can use this to detect errors but now to correct them:
we can use the Majority Vote System this involves sending data three times. We can then take the most common digit for each bit recieved to find out the correct data.
e.g. we try to transmit: 01100110
So we get back:
01100110
01000110
01101010
in red we can see the errors (least common digits)
we can then use the common digits to repair the data.
The only disadvantage of this is that we have to send data three times...
Hamming Distance
This is the distance required to change one string into another. thus finding the distance between the two stings.
e.g. 1110 isn't the same as 1111
to change 1110 to 1111 you need to change the least significant figure to 1
1 move required (1 digit needed changing)
the hamming distance between:
1011101 and 1001001 is 2
These can be represented as images too!
This being an example of a 3 bit cube
This is a hypercube for 4 bits. you can find the distance using these diagrams by taking the shortest route from one set of bits to another for each black circle you go past that is 1 extra to the distance.
Gray Code aka "Reflected Binary Code":
if one switch has 2 states: on and off
and these are coded as 011 and 100
using hammings distance we know that there is a distance of 3 so between the states 011 and 100 we have: 001 and 101
(This would look like this: 011 — 001 — 101 — 100)
This means we cannot tell if the "real" posistion is 011,001, 101 or even 100.
(This would look like this: 011 — 001 — 101 — 100)
This means we cannot tell if the "real" posistion is 011,001, 101 or even 100.
"The reflected binary code solves this problem by changing only one switch at a time, so there is never any ambiguity of position"
Dec Gray Binary
0 000 000
1 001 001
2 011 010
3 010 011
4 110 100
5 111 101
6 101 110
7 100 111
0 000 000
1 001 001
2 011 010
3 010 011
4 110 100
5 111 101
6 101 110
7 100 111
The gray system means that the position change to get to the next code (hammings distance) is only 1, Meaning that there are no "transision" codes between when a switch is changed.
This means grays code goes up in hammings distance of 1 instead of using natural binary:
64 32 16 8 4 2 1
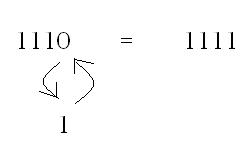


Good summary of parity checking - well done for including Majority Vote - most people forgot that one
ReplyDelete